Edward Nelson (born May 4, 1932, in Decatur, Georgia, dead September 10, 2014 in Princeton, USA) was a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic. In mathematical logic, he is noted especially for his “internal set theory”, and his controversial views on ultrafinitism and the consistency of arithmetic. He has also written on the relationship between religion and mathematics.
Career
Nelson received his Ph.D. in 1955 from the University of Chicago, where he worked with Irving Segal. He was a member of the Institute for Advanced Study from 1956–1959. He has held a position at Princeton University from 1959 to the present, attaining the rank of professor there in 1964.
In 1995 he was awarded by the American Mathematical Society with the prestigious Steele Prize for Seminal Contribution
to Research.
Early work
Nelson has made contributions to the theory of infinite dimensional group representations, the mathematical treatment of quantum field theory, the use of stochastic processes in quantum mechanics, and the reformulation of probability theory in terms of non-standard analysis.
For many years he worked on mathematical physics and probability theory, and still has a residual interest in these fields, particularly in possible extensions of stochastic mechanics to field theory.
In 1950, Nelson formulated a popular variant of the four color problem. What is the chromatic number, denoted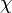 
, of the plane? In more detail, what is the smallest number of colors sufficient for coloring the points of the Euclidean plane in such a way that no two points of the same color are unit distance apart? We know by simple arguments that 4 ≤ χ ≤ 7. The problem was introduced to a wide mathematical audience by Martin Gardner in his October 1960 Mathematical Games column. The chromatic number problem, also now known as the Hadwiger–Nelson problem, was also a favorite of Paul Erdős, who mentioned it frequently in his problems lectures.
Work on foundations
In recent years he has been working on mathematical logic and the foundations of mathematics. One of his goals is to extend IST (Internal Set Theory—a version of a portion of Abraham Robinson’s non-standard analysis) in a natural way to include external functions and sets, in a way that provides an external function with specified properties unless there is a finitary obstacle to its existence. Other work centers on fragments of arithmetic, studying the divide between those theories interpretable in Raphael Robinson’s Arithmetic and those that are not; computational complexity, including the problem of whether P is equal to NP or not; and automated proof checking.
Publications
- Dynamical theory of Brownian motion. Princeton University Press 1967
- Topics in Dynamics 1: Flows. Princeton University Press 1969
- Tensor analysis. Princeton University Press 1967
- Quantum Fluctuations. Princeton University Press, 1985
- Predicative Arithmetic. Princeton University Press, 1986
- Radically elementary probability theory. Annals of Mathematical Studies, Princeton 1987
Other informations about Nelson works and life can be found in his official web page at the Dept. of Mathematics of Princeton University. Read the Commemoration of Prof. Nelson life and work at Princeton University.
